Bạn đang loay hoay trong việc giải bài tập vì không nhớ công thức tính diện tích hình trụ là như thế nào hay gặp khó khăn trong việc phân biệt các khái niệm mặt trụ, hình trụ, khối trụ. Vậy mời bạn cùng đón đọc bài viết dưới đây của chúng tôi để hiểu hơn về phần nội dung kiến thức này.
Trong các khối hình học, hình trụ là hình khối khá đơn giản nhưng cách tính diện tích hình trụ khá khó nhớ, cùng chúng tôi tìm hiểu công thức tính là gì nhé!
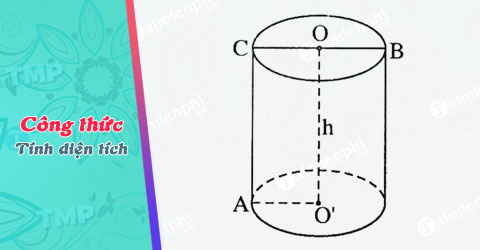
Công thức tính diện tích hình trụ
Công thức tổng quát tính diện tích hình trụ
- Diện tích xung quanh hình trụ:
Sxq = 2. π.r.h
+ Phát biểu bằng lời: Diện tích xung quanh của hình trụ bằng tích 2 lần bán kính trụ với chiều cao và số pi.
- Diện tích toàn phần hình trụ:
Stp = Sxq + Shai đáy = 2. π.r.h + 2.π.r2
+ Phát biểu bằng lời: Diện tích toàn phần hình trụ bằng tổng diện tích xung quanh và diện tích hai đáy.
- Kí hiệu: Sxq, Stp : Lần lượt là diện tích xung quanh và diện tích toàn phần của hình trụ
Shai đáy: Diện tích hai đáy của hình trụ
r: Bán kính đường tròn đáy
h: Chiều cao
- Đơn vị đo: mét vuông (m2)
Bài tập áp dụng :
1. Tính diện tích hình trụ gồm diện tích xung quanh và diện tích toàn phần, biết:
a) r = 5 cm, h = 12 cm
b) r = 3,3 dm, h = 5,1 dm
c) r = 6/7 m, h = 3/2 m
d) r = 10 cm, h = 23 cm
2. Tính diện tích toàn phần của hình trụ có chu vi đáy là 30 cm và chiều cao 6 cm.
3. Hình trụ có diện tích xung quanh bằng 418 cm2, bán kính đáy là 14 cm.
a) Tính chiều cao hình trụ
b) Tính diện tích toàn phần của hình trụ.
* Gợi ý giải bài tập : Với những bài tập này, các em đều sử dụng công thức tính diện tích xung quanh và diện tích toàn phần của hình trụ để giải.
Các kiến thức mở rộng khác bên cạnh công thức diện tích hình trụ
1. Phân biệt các khái niệm mặt trụ, hình trụ và khối trụ
- Mặt trụ (hay còn gọi là mặt tròn xoay): Là hình tròn được tạo nên khi đường thẳng d cố định xoay quanh đường thẳng d' di chuyển linh hoạt và luôn song song, cách d một khoảng bằng R.
+ d' là trục
+ R là bán kính
+ d là đường sinh
=> Ngoài ra: Mặt trụ còn được hiểu là tập hợp tất cả những điểm cách d cố định một khoảng bằng R không đổi.
- Hình trụ: Là hình được giới hạn bởi mặt trụ và hai đường tròn bằng nhau, chính là giao tuyến của mặt trụ và hai mặt phẳng vuông với trục. Nói cách khác, hình trụ được sinh ra khi ta quay một hình chữ nhật một vòng quanh một cạnh cố định của nó.
+ Hai đáy là hai hình tròn bằng nhau và song song với nhau, mỗi hình tròn nằm trên một mặt phẳng khác nhau.
- Khối trụ: Là hình trụ cùng với phần trong của hình trụ đó.
2. Hình trụ nội tiếp và ngoại tiếp mặt cầu
- Khi đáy hình trụ là hai đường tròn trên mặt cầu (S), khi đó hình trụ T được gọi là hình trụ nội tiếp trong mặt cầu (S).
- Khi trục hình trụ là đường kính của mặt cầu (S), khi đó hình trụ T' với bán kính R và chiều cao 2R được gọi là hình trụ ngoại tiếp mặt cầu (S).
Hi vọng những kiến thức mà chúng tôi cung cấp trên đây sẽ giúp ích cho bạn đọc nhất là các em học sinh trong quá trình giải bài tập hình học về tính toán diện tích hình trụ. Các em cũng có thể tham khảo thêm công thức tính thể tích hình trụ, cách tính diện tích hình hộp chữ nhật, hình lập phương,... trong những bài viết khác của chúng tôi.
https://thuthuat.taimienphi.vn/cong-thuc-tinh-dien-tich-hinh-tru-34060n.aspx
Các em cũng cần ôn lại và nắm vững cách tính diện tích hình tròn trong hình học phẳng, đây là kiến thức cơ bản và các em cần ghi nhớ để không gặp khó khăn khi đổi mặt với những bài toán liên quan đến hình tròn.