Khái niệm hình chóp tam giác đều là gì, tính chất và bài tập ví dụ

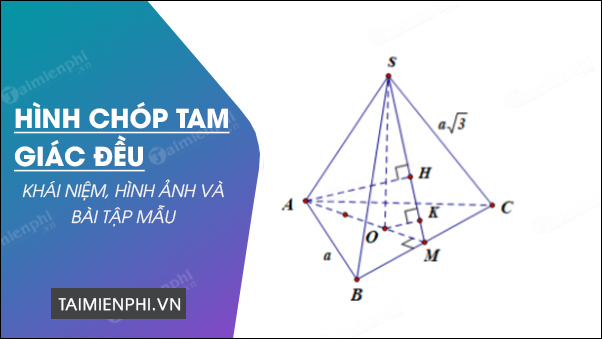
Khái niệm và tính chất của hình chóp tam giác đều

I. Tìm hiểu về hình chóp tam giác đều

1. Khái niệm chóp tam giác đều

- Hình chóp tam giác đều là hình chóp có đáy là tam giác đều, các mặt bên (cạnh bên) đều bằng nhau hay hình chiếu của đỉnh chóp xuống đáy trùng với tâm của tam giác đều.

2. Tính chất

- Đáy của hình chóp này là một tam giác đều
- Các cạnh bên đều bằng nhau
- Các mặt bên của hình chóp này là tam giác cân, không nhất thiết phải là tam giác đều.
- Chân đường cao trùng với tâm đáy (tâm đáy là trọng tâm tam giác)
- Góc được tạo bởi mặt bên và mặt đáy đều bằng nhau
- Góc được tạo bởi cạnh bên và mặt đáy đều bằng nhau.

3. Phân biệt chóp tam giác đều và tứ diện đều

- Tứ diện đều cũng chính là chóp tam giác đều, tuy nhiên trong tứ diện đều, cạnh bên = cạnh đáy nói cách khác ở tứ diện đều tất cả các mặt đều là tam giác đều.

II. Hình ảnh hình chóp tam giác đều

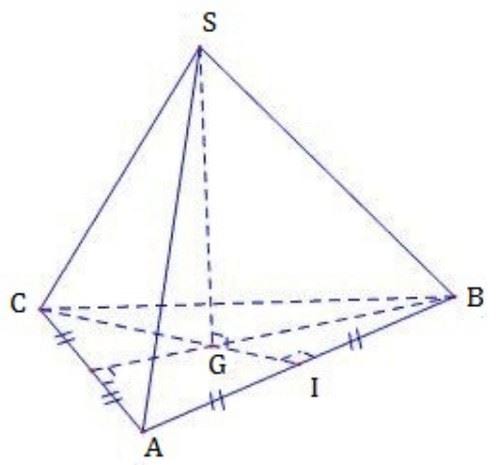
Hình chóp tam giác đều có bao nhiêu đỉnh?

III. Cách vẽ chóp tam giác đều bằng 3 bước đơn giản

Bước 1: Vẽ mặt đáy hình chóp là tam giác đều ABC (nhưng không nhất thiết phải vẽ ba cạnh bằng nhau hoàn toàn mà có thể vẽ tam giác thường), AC vẽ nét đứt
Bước 2: Vẽ hai đường trung tuyến CF và AI giao nhau tại O, O chính là chân đường cao trùng với tâm đáy
Bước 3: Từ O, dựng đường thẳng đứng, ta được đỉnh S, từ S nối với đỉnh A, B, C

=> Hoàn thành cách dựng hình chóp tam giác đều SABC có: SH là đường cao, SA = SB = SC.

Các công thức tính toán liên quan đến chóp tam giác đều

- Công thức tính diện tích hình chóp tam giác đều (mặt đáy):

S = (a2 x √3) : 4

- Công thức tính đường cao của tam giác đều:

h = (a x √3) : 2

- Công thức tính thể tích chóp tam giác đều:

V = 1/3. h. Sđáy

- Giải thích kí hiệu:

+ S là diện tích của tam giác đều
+ S đáy là diện tích đáy
+ a là 1 cạnh tam giác
+ h là đường cao

Bài tập hình chóp tam giác đều: Cho hình chóp tam giác đều SABC có đáy cạnh b, mặt bên tạo với đáy một góc 60 độ. Tính thể tích khối chóp SABC.

* Hướng dẫn:

- Các em dựng khối chóp tam giác đều SABC như hình minh họa bên trên.
- Gọi điểm I là tâm đáy => SI vuông góc với mặt phẳng đáy ABC.

=> VSABC = 1/3. SI. S_{tam giác ABC}

- Tính: S_ABC = b2√3 : 4
- Tính SI:

+ Góc tạo bởi mặt bên (SBC) và mặt đáy (ABC) = góc SDI = 60 độ

Ta có: ID = 1/3. AD = 1/3. (b√3 : 2) = b : 2√3 (tính chất đường cao, đường trung tuyến AD trong tam giác đều)

+ Xét tam giác vuông SID có: tanSDI = đối/kề = SI : ID

=> SI = (b : 2√3) . √3
=> SI = b/2
=> V_SABC = 1/3 . b/2. b2√3 : 4 = b3√3/24 (đvtt).

-------------------HẾT--------------------

Qua bài viết của chúng tôi, chắc hẳn bạn đọc đã hiểu rõ hơn về hình chóp tam giác đều là gì, cách vẽ đơn giản cũng như công thức và cách làm một số bài toán về chóp tam giác đều. Bạn cũng có thể chủ động tự giải một số bài tập dựa trên những gợi ý của chúng tôi. Bên cạnh đó các em cũng cần củng cố thêm kiến thức cách tính diện tích tam giác, đây là kiến thức cơ bản các em cần nắm vững.

https://thuthuat.taimienphi.vn/hinh-chop-tam-giac-deu-la-gi-hinh-anh-va-bai-toan-mau-35499n.aspx
Ngoài ra các bạn có thể tham khảo thêm bài viết công thức tính thể tích hình chóp trong chuỗi bài tập về hình chóp để giải toán hiệu quả.