Nắm bắt cách tính đường chéo hình vuông là điều cần thiết, đây là kiến thức cơ bản giúp các bạn dễ dàng làm các bài tập liên quan hình vuông. Nếu bạn quên thì có thể tham khảo bài viết sau đây để bổ sung các kiến thức cần thiết.
Do hình vuông là trường hợp đặc biệt của hình tứ giác, hình thang, hình chữ nhật ... nên bạn có thể áp dụng cách tính đường chéo hình chữ nhật vào đường chéo của hình vuông hoặc áp dụng trực tiếp theo cách tính đường chéo hình vuông dưới đây.
Công thức tính đường chéo hình thang, hình vuông, hình chữ nhật
I. Công thức tính đường chéo hình vuông
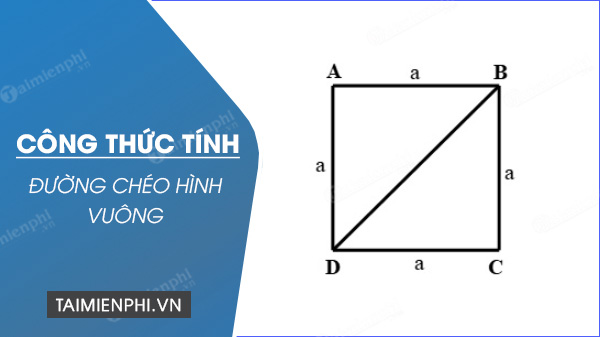
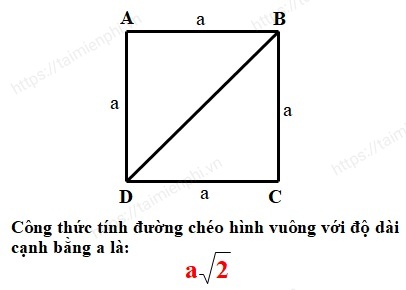
Cho hình vuông ABCD, các cạnh AB = BC = CD = DA = a, tính hình chéo BD, AC.

II. Những điều cần biết về hình vuông
Hình vuông là hình tứ giác đều hay hình chữ nhật có các cạnh đều bằng nhau hoặc hình thoi có hai đường chéo bằng nhau.
1. Tính chất của hình vuông
- Hai đường chéo bằng nhau và vuông góc với nhau, cắt nhau tại trung điểm của mỗi đường.
- Tâm của đường tròn nội tiếp và ngoại tiếp trùng với giao điểm hai đường chéo hình vuông.
- Một đường chéo sẽ chia hình vuông với hai phần bằng nhau.
- Giao của đường trung tuyến, trung trực của các cạnh, đường phân giác đều đồng quy tại một điểm.
- Có các tính chất của hình thoi, hình bình hành, hình chữ nhật.
2. Đường chéo hình vuông có tính chất gì?
- Hai đường chéo bằng nhau.
- Hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường.
- Đường chéo chia hình vuông thành hai hình và hình đó chính là tam giác vuông cân.
3. Dấu hiệu nhận biết hình vuông
- Hình chữ nhật có hai cạnh kề bằng nhau.
- Hai đường chéo của hình chữ nhật vuông góc với nhau là hình vuông.
- Hình thoi có 1 góc vuông.
- Hình thoi có hai đường chéo bằng nhau.
III. Bài tập ví dụ tính đường chéo hình vuông
Cho hình vuông ABCD có cạnh a = 5cm, tính đường chéo AC, BD?
Giải:

https://thuthuat.taimienphi.vn/cach-tinh-duong-cheo-hinh-vuong-56200n.aspx
Trên đây là cách tính đường chéo hình vuông, các bạn cùng tham khảo để có thể vận dụng vào bài học, các bài tập liên quan tới tính diện tích hình vuông dễ dàng và hiệu quả.