Các bài tập Toán lớp 5 thường liên quan tới cách tính đường cao trong tam giác, tính diện tích tam giác, tính các cạnh ... nên việc nắm bắt công thức, cách tính đường cao tam giác là rất cần thiết, giúp bạn giải các dạng bài tập hình tam giác khác nhau trở nên dễ dàng hơn rất nhiều.
Tính đường cao trong tam giác là dạng bài tập mà các bạn học sinh thường gặp phải khi làm và học toán, liên quan tới cả tính diện tích của tam giác. Nếu như bạn chưa biết về công thức tính đường cao hình tam giác thì bạn nên tham khảo bài viết cách tính đường cao trong tam giác cân, đều, vuông sau đây.
Công thức tính đường cao trong tam giác vuông, tam giác đều, tam giác cân
I. Công thức tính đường cao trong tam giác
1. Trường hợp 1: Tam giác thường
Công thức tính chiều cao hình tam giác:
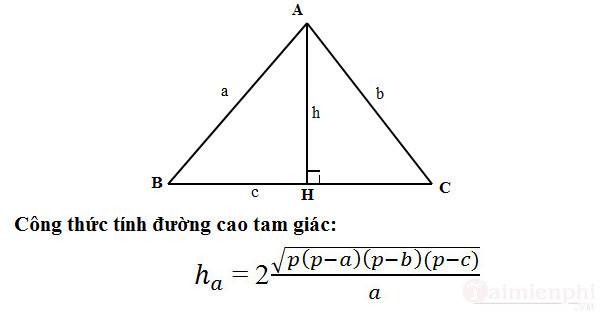
Trong đó:
- a, b, c là độ dài các cạnh trong tam giác.
- h là chiều cao trong tam giác.
- p là nửa chu vi tam giác có công thức là p = (a + b + c) : 2.
2. Trường hợp 2: Tam giác cân
Giả sử các bạn có tam giác ABC cân tại A và đường cao AH vuông tại H như hình dưới đây.

Vì ABC cân tại A nên đường cao AH đồng thời là đường trung tuyến nên:
HB = H C= BC/2.
Áp dụng định lý Pi-ta-go cho tam giác vuông AHB vuông tại H ta có:

Từ đó, bạn chỉ cần tính các ẩn số trong công thức là có thể tính đường cao tam giác đều ABC.
3. Trường hợp 3: Tam giác đều
Cách tính đường cao trong tam giác đều như sau:

4. Trường hợp 4: Tam giác vuông

Trong đó, tam giác vuông ABC vuông tại A, đường cao AH cắt BC tại H:
a, b, c là các cạnh của tam giác vuông như trên hình.
b' là đường chiếu của cạnh b trên cạnh huyền
c' là đường chiếu của cạnh c trên cạnh huyền
h là đường cao AH
II. Bài tập ví dụ về tính đường cao trong tam giác
Ví dụ 1: Cho tam giác ABC vuông tại A, có đường cao AH, cho AB : AC = 3 : 4, AB + AC = 21cm.
a. Tính các cạnh của tam giác ABC.
b. Tính đường cao AH.
Giải
Các em có thể áp dụng cách tính đường cao trong tam giác vuông để giải bài toán.

Ví dụ 2: Cho tam giác ABC, cạnh AB = 4 cm, cạnh BC = 7 cm, cạnh AC = 5 cm. Tính đường cao AH kể từ A cắt BC tại H và tính diện tích ABC.
Giải:

Khi các bạn tính đường cao trong tam giác, bạn có thể tính được diện tích tam giác . tìm được độ dài các cạnh, tính góc trong tam giác đơn giản và dễ dàng hơn rất nhiều.
https://thuthuat.taimienphi.vn/cach-tinh-duong-cao-trong-tam-giac-56202n.aspx
Tam giác đều là là trường hợp đặc biệt của hình tam giác, các bạn cách tính đường cao trong tam giác đều dựa vào công thức tính đường cao trong tam giác.