Cùng tham khảo hướng dẫn chi tiết và đầy đủ nhất về công thức, cách tính diện tích xung quanh và diện tích toàn phần, thể tích hình nón cụt để có thể áp dụng chính xác nhất khi giải toán trong sách hoặc các bài toán thực tế.
Công thức tính diện tích và thể hình nón cụt được áp dụng khá nhiều trong các bài toán hình học cơ bản. Khác với công thức tính diện tích hình nón thông thường, hình nón cụt có hai mặt đỉnh và đáy đều phẳng dẫn tới công thức áp dụng cũng rất khác.
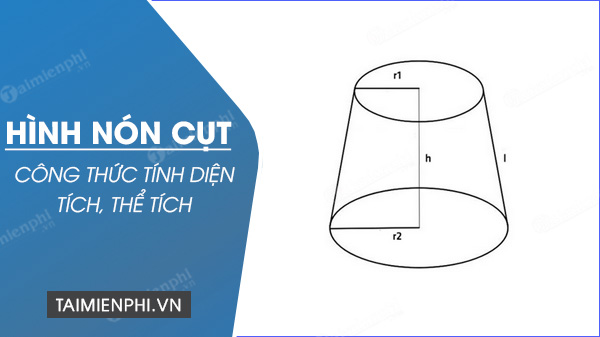
Cách tính thể tích, diện tích của hình nón cụt
Tuy nhiên nếu biết cách phân biệt giữa hai loại hình học này, việc tính diện tích và thể tích hình nón cụt sẽ khá dễ dàng. Hình nón cụt cũng được áp dụng cùng với công thức tính diện tích và thể tích hình trụ do sự tương quan hình học.
Tổng hợp công thức tính diện tích, thể tích hình nón cụt
1. Công thức và cách tính diện tích hình nón cụt
1.1. Công thức tính diện tích toàn phần của hình nón cụt:
Stp = π.(r1 + r2).l + πr12 + πr22
Trong đó:
- r1, r2: Bán kính mặt đáy của hình nón cụt. Mặt đáy của hình nón cụt là mặt tròn. Các bạn có thể tìm hiểu mặt đáy này bằng cách xem thêm trên Wikipedia bài viết về mặt tròn.
- l: Độ dài đường sinh của hình nón cụt.
- π: số Pi (xấp xỉ 3,14).
- Ví dụ cách tính diện tích toàn phần hình nón cụt
Cho một hình nón cụt có bán kính hai mặt đáy r1 và r2 lần lượt bằng 5cm và 7cm. sinh l nối từ đỉnh tới đáy hình nón là 6cm. Hỏi diện tích toàn phần của hình nón này bằng bao nhiêu?
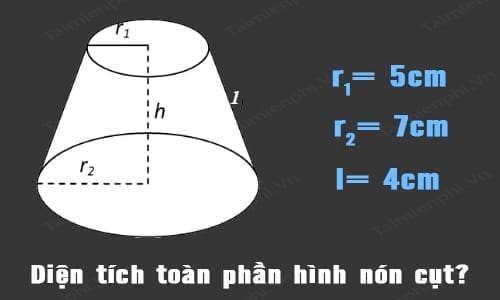
Áp dụng theo công thức tính diện tích toàn phần của hình nón cụt, ta có r1 = 5cm, r2 = 7cm và chiều dài đường sinh l = 6cm. Suy ra diện tích toàn phần của hình nón cụt khi áp dụng theo công thức như sau:
Stp = π.(5 + 7).4 + (π.52 + π.72) = π.12.4 + (π.25 + π.49) = 383,08 (cm2).
Như vậy diện tích toàn phần của hình nón cụt này bằng xấp xỉ 383,08 cm2.
1.2. Công thức tính diện tích xung quanh hình nón cụt:
Sxq = π.(r1 + r2).l
Trong đó:
- r1, r2: Hai mặt đáy của hình nón cụt
- l: Đường sinh của hình nón cụt
- π: số Pi (xấp xỉ 3,14)
- Ví dụ cách tính diện tích xung quanh hình nón cụt:
Cùng áp dụng với bài toán trên, ta có cách tính diện tích xung quanh hình nón cụt được áp dụng theo công thức sau: r1 = 5cm , r2 = 7cm và đường sinh l = 6cm

Sxq = π.(r1 + r2).l = π.(5 +7).6 ~ 226 cm2.
2. Công thức và cách tính thể tích hình nón cụt
- Công thức tính thể tích hình nón cụt
V = 1/3π.h.(r12 + r1.r2+ r22)
Trong đó:
- r1, r2 : Hai mặt đáy của hình nón cụt.
- h : Chiều cao nối giữa hai đáy của hình nón cụt.
- π: số Pi (xấp xỉ 3,14).
- Ví dụ cách tính thể tích hình nón cụt
Cho một hình nón cụt có bán kính hai mặt đáy r1 và r2 lần lượt bằng 5cm và 9cm. Chiều cao nối giữa hai bán kính mặt đáy này có độ dài 8cm. Hỏi diện tích toàn phần của hình nón này bằng bao nhiêu?

Áp dụng theo công thức tính thể tích hình nón cụt ta có: r1 = 5cm, r2 = 9cm, h = 8cm.
V = 1/3π.8. (52 + 5.9 +92) = 1264,37 (cm3).
Như vậy thể tích của hình nón cụt này bằng xấp xỉ 1264,367 cm3.
Tổng hợp công thức tính diện tích và thể tích hình nón cụt là những công thức thường gặp nhất trong các bài toán hình học từ đơn giản đến phức tạp, hơn nữa bạn có thể sử dụng kết hợp giữa công thức tính diện tích và thể tích hình nón cụt và công thức tính thể tích hình trụ, đặc biệt trong các bài toán phức hợp, giao nhau giữa nhiều hình.
Cùng với công thức tính thể tích hình trụ, tổng hợp công thức tính diện tích hình tam giác, hình vuông và hình chữ nhật cũng được sử dụng khác phổ biến. Tuy nhiên khác với hình học không gian, hình học phẳng và cách tính diện tích tam giác, hình vuông và hình chữ nhật rất khác. Do đó điều quan trọng nhất, đó là bạn cần phân biệt được hình học trong mặt phẳng và hình học không gian.
Khi học hình nón cụt, chắc chắn bạn cũng sẽ học qua cách tính thể tích hình nón (Có chóp nhọn), chính vì sự khác nhau này nên cách tính thể tích hình nón sẽ khác đôi chút với cách tính thể tích hình nón cụt bên trên.
Hình cầu cũng là một trong các hình mà bạn phải nghiên cứu trong chương trình học của mình, giống với các hình học khác, thì trong hình cầu cũng có cách tính diện tích và thể tích, để có cách tính thể tích hình cầu chuẩn xác nhất, mời các bạn theo dõi bài viết cách tính thể tích hình cầu mà Taimienphi đã giới thiệu. Chúc các bạn thành công!
https://thuthuat.taimienphi.vn/cach-tinh-the-tich-hinh-non-cut-dien-tich-xung-quanh-va-dien-tich-toan-phan-cong-thuc-tinh-22980n.aspx
Chúc các bạn thành công!