Phương trình mặt phẳng - Toán Hình học lớp 12

Taimienphi.vn sẽ tổng hợp kiến thức Phương trình mặt phẳng lớp 12 đầy đủ và chi tiết nhất cùng với các ví dụ minh họa giúp các em học sinh có thể củng cố, bổ sung lại kiến thức một cách có hệ thống và hiệu quả nhất.

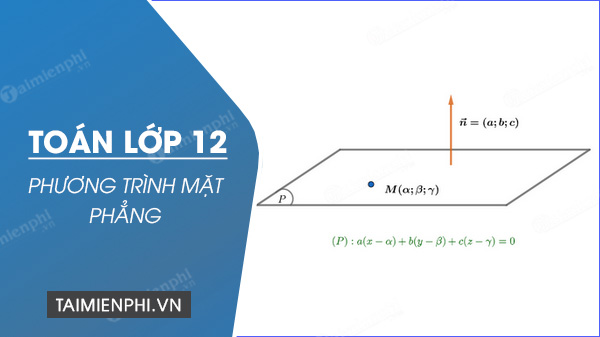
Lý thuyết, công thức, các dạng bài phương trình mặt phẳng - Toán lớp 12.

1. Véctơ pháp tuyến của mặt phẳng

2. Phương trình mặt phẳng

3. Vị trí tương đối của hai mặt phẳng

4. Khoảng cách từ một điểm đến một mặt phẳng

5. Góc giữa hai mặt phẳng

Nhận xét: Muốn viết phương trình mặt phẳng thì có hai phương pháp chính
Phương pháp 1: Xác định 1 điểm mà mặt phẳng đi qua và 1 vectơ pháp tuyến.
Phương pháp 2: Xác định 1 vectơ pháp tuyến và tham số D trong phương trình dạng tổng quát Ax + By + Cz + D = 0.

6. Các dạng bài tập cơ bản

Dạng 1: Viết phương trình mặt phẳng bằng cách xác định vectơ pháp tuyến

Ví dụ 2: Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M (0; 1; 2) và song song với mặt phẳng (Q): 2x - 4y + 2 = 0.

Hướng dẫn giải:

Lời giải:

2(x - 0) - 4(y - 1) + 0.(z - 2) = 0
⇔2x - 4y + 4 = 0
⇔x - 2y + 2 = 0

Dạng 2: Viết phương trình mặt phẳng liên quan đến khoảng cách

Ví dụ 3: Trong không gian hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng (Q): x + 2y - 2z + 1 = 0 và cách (Q) một khoảng bằng 3.

Hướng dẫn giải:
1. Trên mặt phẳng (Q) chọn một điểm M.
2. Do mặt phẳng (P) song song với mặt phẳng (Q) nên mặt phẳng (P) có dạng: Ax + By + Cz + D' = 0 (D' ≠ D).
3. Sử dụng công thức khoảng cách d((P),(Q)) = d(M,(Q)) = k để tìm D'.

Lời giải:
Trên mặt phẳng (Q) chọn điểm M (-1; 0;0).
Do mặt phẳng (P) song song với mặt phẳng (Q) nên phương trình mặt phẳng (P) có dạng: x + 2y - 2z + D = 0 (D ≠ 1).
Vì khoảng cách giữa 2 mặt phẳng (P) và (Q) bằng 3 nên ta có:

Vậy có 2 phương trình mặt phẳng (P) thỏa mãn yêu cầu đề bài là
x + 2y - 2z + 10 = 0
x + 2y - 2z - 8 = 0

Dạng 3: Viết phương trình mặt phẳng liên quan đến mặt cầu

Ví dụ 4: Trong không gian hệ tọa độ Oxyz, cho hình cầu (S): (x - 1)² + (y - 2)² + (z - 3)² = 1. Viết phương trình mặt phẳng (P) chứa trục Oz và tiếp xúc với (S).

Hướng dẫn giải:

Lời giải:

Dạng 4: Viết phương trình mặt phẳng liên quan đến góc

Ví dụ 5: Trong không gian hệ tọa độ Oxyz, gọi (P) là mặt phẳng chứa trục Oy và tạo với mặt phẳng (Q): y + z + 1 = 0 góc 600. Phương trình mặt phẳng (P) là:

Hướng dẫn giải:

Lời giải:

Giả sử phương trình mặt phẳng (P) có dạng: Ax + By + Cz + D = 0

(A² + B² + C² ≠ 0).

Lại có mặt phẳng (P) tạo với mặt phẳng (Q) một góc bằng 60 độ nên ta có:

Chọn C = 1, ta có A = ± 1

x + z = 0
-x + z = 0

https://thuthuat.taimienphi.vn/phuong-trinh-mat-phang-toan-hinh-hoc-lop-12-69279n.aspx
Các em học sinh nhớ cập nhật đầy đủ kiến thức phương trình mặt phẳng Toán hình học lớp 12 trên đây. Bên cạnh đó, các em nên làm bài tập thường xuyên để củng cố kiến thức, khi gặp bài toán này có thể giải quyết nhanh chóng.